Replicator dynamics¶
Motivating example: The Hawk Dove Game¶
Consider a population of animals. These animals when they interact will always share their food. Due to a genetic mutation, some of these animals may act in an aggressive manner and not share their food. If two aggressive animals meet they both compete and end up with no food. If an aggressive animal meets a sharing one, the aggressive one will take most of the food.
These interactions can be represented using the matrix \(A\):
In this scenario: what is the likely long term effect of the genetic mutation?
Over time will:
The population resist the mutation and all the animals continue to share their food.
The population get taken over by the mutation and all animals become aggressive.
A mix of animals are present in the population some act aggressively and some share.
To answer this question we will assume a vector \(x\) represents the population. In this case:
\(x_1\) represents the proportion of the population that shares.
\(x_2\) represents the proportion of the population that acts aggressively.
Note that as the components of \(x\) are proportions of the population this implies:
We will also assume that any given individual in the population is playing a strategy \(\chi\), which:
shares \(\chi_1\) proportion of the time.
acts aggressively \(\chi_2\) proportion of the time.
The overall fitness of an individual in the population is then given by their expected utility (as given by \(A\)) as they interact with the population:
We can in fact write down the fitness corresponding to each action (sharing or being aggressive):
The average fitness in the population is then given by:
To understand how the population will evolve relative to their fitness the following differential equation will be used:
In our case the differential equations are:
where:
This differential equation can then be solved numerically to show the evolution of the population over time. We can see that it looks like in our particular situation the mutation stays within the population and a mix of both sharing and aggressive animals will coexist.
(Source code, png, hires.png, pdf)
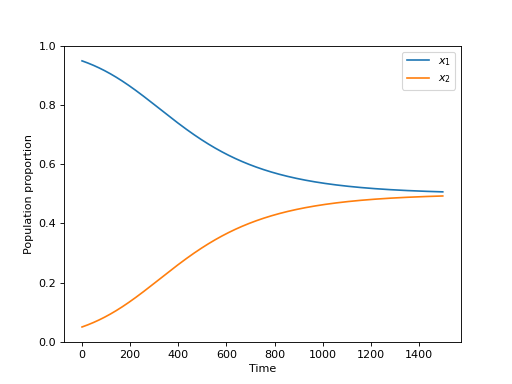
The replicator dynamics equation¶
Given a population with \(N\) types of individuals. Where the fitness of an individual of type \(i\) when interacting with an individual of type \(j\) is given by \(A_{ij}\) where \(A\in\mathbb{R}^{N \times N}\). The replicator dynamics equation is given by:
where:
where \(f_i\) is the population dependent fitness of individuals of type \(i\):
Note that there are equivalent linear algebraic definitions to the above:
Question
For Rock Paper Scissors, what is the replicator dynamics equation?
Answer
Recalling that rock paper scissors has a payoff matrix \(A\) given by:
For a general population vector \(x\) the population dependent fitness \(f\) is given by:
The average fitness is given by:
\[\phi = x^T f = x_1(x_3 - x_2) + x_2(x_1 - x_3) + x_3(x_2 - x_1)\]
The replicator dynamics equation is then given by:
Closer inspection of \(\phi\) gives: \(\phi=0\) thus:
Stability of the replicator dynamics equation¶
Stability of the replicator dynamics equation is achieved when \(\frac{dx_i}{dt} = 0\) for all \(i\).
For a population vector \(x^*\) for which \(\frac{dx^*_i}{dt} = 0\) for all \(i\) the population will not change without some other effect. This is referred to as a stable population.
Question
For the following games, what are the stable populations?
Answer
The replicator dynamics equation for this game are:
For them all to be 0, this requires:
\(x_1=0\) or \(x_2=x_3\)
\(x_2=0\) or \(x_1=x_3\)
\(x_3=0\) or \(x_1=x_2\)
Which, through inspection in turn requires:
\(x_1\ne 0\) and \(x_2=x_3=0\) or
\(x_2\ne 0\) and \(x_1=x_3=0\) or
\(x_3\ne 0\) and \(x_1=x_2=0\) or
\(x_1=x_2=x_3\).
Given that \(x_1+x_2+x_3=1\) this leaves us with 4 possible stable populations:
\(x=(1, 0, 0)\)
\(x=(0, 1, 0)\)
\(x=(0, 0, 1)\)
\(x=(1 / 3, 1 / 3, 1 / 3)\)
The following plot shows each of the above populations which no longer change over time:
(Source code, png, hires.png, pdf)
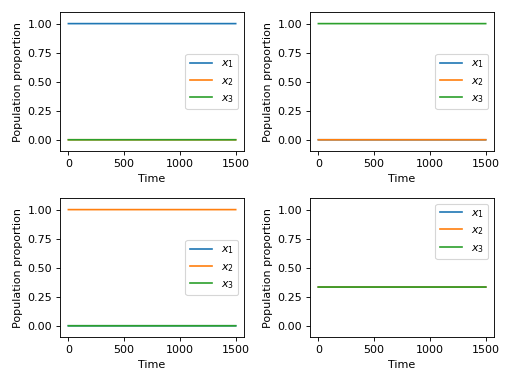
The replicator dynamics equation for this game are:
\[\begin{split}\begin{align*} \frac{dx_1}{dt} &= x_1(2x_1 + x_2 - \phi)\\ \frac{dx_2}{dt} &= x_2(3x_1 - \phi) \end{align*}\end{split}\]where:
\[\phi=x_1(2x_1 + x_2) + x_2(3x_1)\]substituting \(x_2 = 1 - x_1\) here gives:
\[\begin{split}\begin{align*} \frac{dx_1}{dt} &= x_1(x_1 - 1)(2x_1-1)\\ \frac{dx_2}{dt} &= -x_1(x_1 - 1)(2x_1-1) \end{align*}\end{split}\]
For them both to be 0, this requires:
\(x_1=0\) or
\(x_1=1\) or
\(x_1=1/2\)
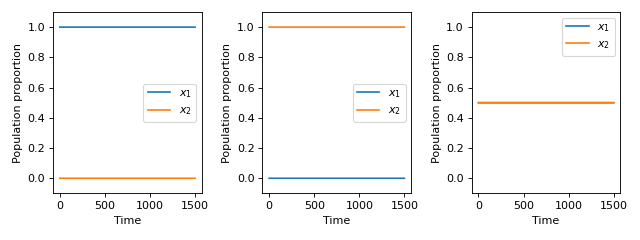
Recalling the substition that \(x_2=1 - x_1\) this leaves us with 3 possible stable populations:
\(x=(1, 0)\)
\(x=(0, 1)\)
\(x=(1/2, 1/2)\)
The following plot shows each of the above populations which no longer change over time:
(Source code, png, hires.png, pdf)
Evolutionary stable strategies¶
Evolutionary stable strategies are strategies that when adopted by an entire population are resistant to an alternative strategy that is initially rare.
By definition an evolutionary stable strategy corresponds to a stable population.
For the hawk dove game there are 3 stable populations:
\(x=(1, 0)\)
\(x=(0, 1)\)
\(x=(1 / 2, 1 / 2)\)
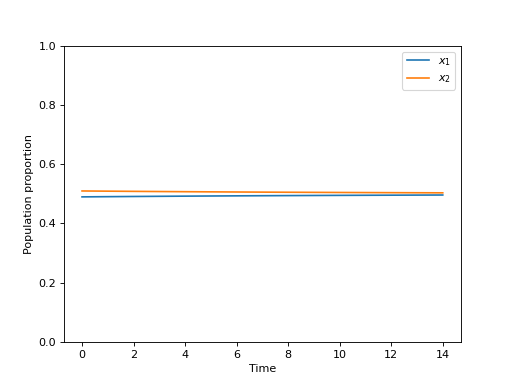
However, if a small deviation is made from the first two populations then the population does not “resist”. For example, we consider the initial population \(x=(1, 0)\) and introduce a small population aggressive behaviours to have: \(x = (1 - \epsilon, \epsilon)\) where \(\epsilon>0\). The plot below shows this with \(\epsilon=10 ^ -5\):
(Source code, png, hires.png, pdf)
This is also what happens if we start with a population of aggressive animals: We consider the initial population \(x=(0, 1)\) and introduce a small population aggressive behaviours to have: \(x = (\epsilon, 1 - \epsilon)\) where \(\epsilon>0\). The plot below shows this with \(\epsilon=10 ^ {-5}\):
(Source code, png, hires.png, pdf)
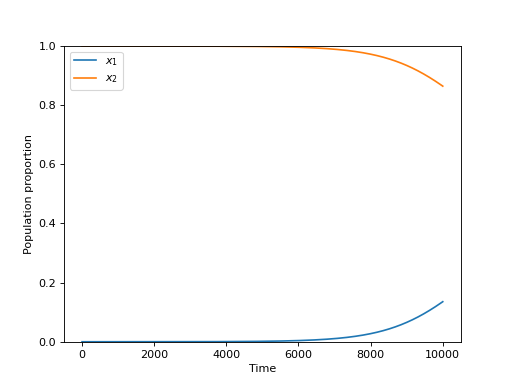
However, this is not the case with the third stable population: \(x=(1 / 2, 1 / 2)\). The plot below shows \(x=(1 / 2 - \epsilon, 1 / 2 + \epsilon)\) with \(\epsilon=10^{-2}\):
(Source code, png, hires.png, pdf)
These observations can be confirmed analytically. Information on this can be found in [Fudenberg1998], [Webb2007] and [Nowak2006].
The replicator equations were first presented in [Maynard1974].
The replicator-mutation dynamics equation¶
An extension of the replicator equation is to allow for mutation [Komarova2004]. In this case reproduction is imperfect and individuals of a given type can give individuals of another.
This is expressed using a matrix \(Q\) where \(Q_{ij}\) denotes the probability of an individual of type \(j\) is produced by an individual of type \(i\).
In this case the replicator equation can be modified to give the replicator-mutation equation:
where, as before:
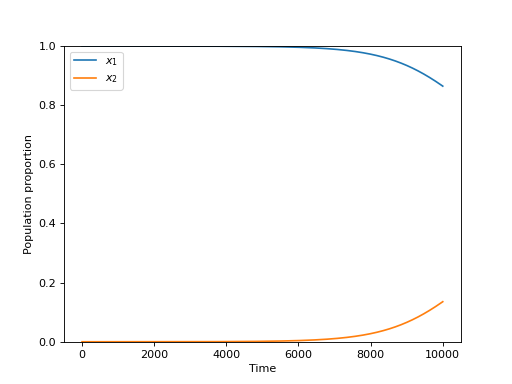
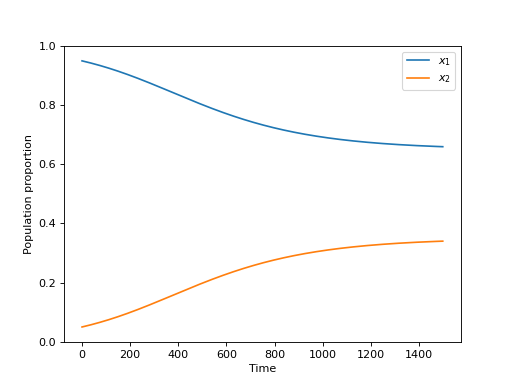
This can modify emergent behaviour. For the Hawk Dove game if there is a 10% change that aggressive individuals will produce sharing ones the matrix \(Q\) is given by:
The plot below shows the evolution of the system:
(Source code, png, hires.png, pdf)
Question
Show that for \(Q=I_N\) (the identity matrix of size \(N\)) the replicator-mutation equation corresponds to the replicator equation.
Answer
The replicator-mutation equation is:
As \(Q=I_N\):
This gives:
As required.
Exercises¶
Consider a population with two types of individuals: \(x=(x_1, x_2)\) such that \(x_1 + x_2 = 1\). Obtain all the stable distribution for the system defined by the following fitness functions:
\(f_1(x)=x_1 - x_2\qquad f_2(x)=x_2 - 2 x_1\)
\(f_1(x)=x_1x_2 - x_2\qquad f_2(x)=x_2 - x_1 + 1/2\)
\(f_1(x)=x_1 ^ 2 \qquad f_2(x)=x_2^2\)
For the following games, obtain all the stable distributions for the evolutionary game:
\(A = \begin{pmatrix}2 & 4 \\ 5 & 3\end{pmatrix}\)
\(A = \begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}\)
Using Nashpy¶
See Use replicator dynamics for guidance of how to use Nashpy to obtain numerical solutions of the replicator dynamics equation. See Use replicator dynamics with mutation for guidance of how to use Nashpy to obtain numerical solutions of the replicator-mutation dynamics equation.This is what is used to obtain all the plots above.