The Emergence of Cooperation¶
Motivating example: can cooperation emerge in a short time frame?¶
The repeated Prisoners Dilemma is a model of direct reciprocity.
The first action corresponds to acting in the interest of all individuals (this is often referred to as Cooperate).
The second action corresponds to acting in ones own self interest (this is often referred to as Defect).
In a population of individuals, is it possible for self interest to not become the norm?
To answer this question we can consider the Iterated Prisoners Dilemma as a repeated game where individuals have two consecutive interactions. The incentive to initially acting selflessly is that the other individual will do the same in the second interaction.
Recalling Strategies in a repeated game the strategies in this case must map histories of play to actions. The possible histories of play are:
Row strategies are thus of the form:
Cooperate unconditionally:
Defect unconditionally:
Start by cooperating and then repeat the action of the opponent:
The strategy space when repeating the game twice corresponds to 32 different strategies. We can see how these 32 strategies interact in an evolutionary setting using replicator dynamics.
(Source code, png, hires.png, pdf)
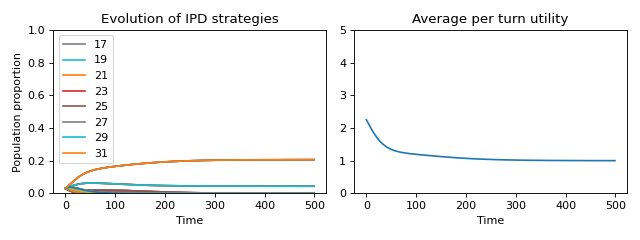
The legend shows the index in the strategy space of the strategies that have a final proportion larger than \(10 ^ {-2}\). The average utility plot gives us the answer to our question: the average per turn utility is 1 which implies that the strategies that survive the evolutionary process are the ones that act selfishly.
The immediate conclusion is somewhat disappointing: how can a society emerge in which individuals will do what is best for the collective?
This question can be better answered by considering a much larger strategy space corresponding to more repetitions of the prisoners dilemma.
The General form of the Prisoners Dilemma¶
The general form is:
with the following constraints:
The first constraint ensures that the second action “Defect” dominates the first action “Cooperate”.
The second constraint ensures that a social dilemma arises: the sum of the utilities to both players is best when they both cooperate.
This game is a good model of agent (human, etc) interaction: a player can choose to take a slight loss of utility for the benefit of the other play and themselves.
Question
Under what conditions is the following game a Prisoners Dilemma:
Answer
This is a Prisoners Dilemma when:
and:
Both of these equations hold for \(\mu>0\). This is a convenient form for the Prisoners Dilemma as it corresponds to a 1 dimensional parametrization.
As a single one shot game there is not much more to say about the Prisoner’s dilemma. It becomes fascinating when studied as a repeated game.
Axelrod’s tournaments¶
In 1980, Robert Axelrod (a political scientist) invited submissions to a computer tournament version of an iterated prisoners dilemma. This was described in a 1980 paper [Axelrod1980].
14 strategies were submitted.
Round robin tournament with 200 stages including a 15th player who played uniformly randomly.
Some complicated strategies, including for example a strategy that used a \(\chi^2\) test to try and identify strategies that were acting randomly. You can read more about this tournament here: http://axelrod.readthedocs.io/en/stable/reference/overview_of_strategies.html#axelrod-s-first-tournament
The winner (average score) was in fact a straightforward strategy: Tit For Tat. This strategy starts by cooperating and then repeats the opponents previous move.
The 15 by 15 payoff matrix (rounded to 1 digit) that corresponds to this tournament is:
We see that the first 8 strategies all cooperate with each other (getting a utility of 3).
These 15 strategies are a small subset of the strategy space for the iterated prisoners dilemma with \(T=200\) repetitions. As before, we can see how these 15 strategies interact in an evolutionary setting using replicator dynamics.
(Source code, png, hires.png, pdf)
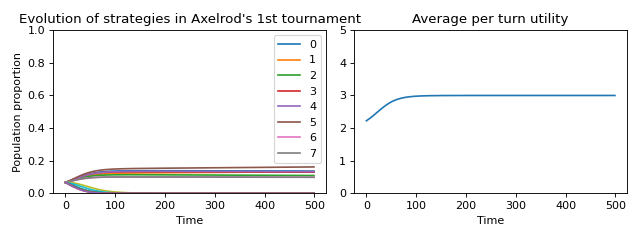
It is evident here that cooperation emerges from this strategy space.
The fact that Tit For Tat won garnered a lot of research (still ongoing) as it showed a mathematical model of how cooperative behaviour can emerge in complex situations. However, recent research has shown that Tit For Tat is not a universally strong strategy [Knight2018], [Harper2017], [Press2012].
Exercises¶
Justify if the following games are Prisoners dilemmas or not:
- \[\begin{split}A = \begin{pmatrix} 3 & 0\\ 5 & 1 \end{pmatrix} \qquad B = \begin{pmatrix} 3 & 5\\ 0 & 1 \end{pmatrix}\end{split}\]
- \[\begin{split}A = \begin{pmatrix} 1 & -1\\ 2 & 0 \end{pmatrix} \qquad B = \begin{pmatrix} 1 & 2\\ -1 & 0 \end{pmatrix}\end{split}\]
- \[\begin{split}A = \begin{pmatrix} 1 & -1\\ 2 & 0 \end{pmatrix} \qquad B = \begin{pmatrix} 3 & 5\\ 0 & 1 \end{pmatrix}\end{split}\]
- \[\begin{split}A = \begin{pmatrix} 6 & 0\\ 12 & 1 \end{pmatrix} \qquad B = \begin{pmatrix} 6 & 12\\ 0 & 0 \end{pmatrix}\end{split}\]
Using Python¶
There is a Python library (axelrod) with over 200 strategies that can be
used to reproduce this work [Knight2016]. You can read the documentation for it
here: http://axelrod.readthedocs.io.