Best responses¶

Motivating example: Best Responses in Matching Pennies¶

\[\begin{split}A = \begin{pmatrix} 1 & -1\\ -1 & 1 \end{pmatrix} \qquad B = \begin{pmatrix} -1 & 1\\ 1 & -1 \end{pmatrix}\end{split}\]

If the row player knows that the column player is playing the strategy \(\sigma_c=(0, 1)\) the utility of the row player is maximised by playing \(\sigma_r=(0, 1)\).

In this case \(\sigma_r\) is referred to as a best response to \(\sigma_c\).

Alternatively, if the column player knows that the row player is playing the strategy \(\sigma_r=(0, 1)\) the column player’s best response is \(\sigma_c=(1, 0)\).

Definition of a best response in a normal form game¶

In a two player game \((A,B)\in{\mathbb{R}^{m\times n}}^2\) a strategy \(\sigma_r^*\) of the row player is a best response to a column players’ strategy \(\sigma_c\) if and only if:

\[\sigma_r^*=\text{argmax}_{\sigma_r\in \mathcal{S}_1}\sigma_rA\sigma_c^T.\]

Where \(\mathcal{S}_1\) denotes the space of all strategies for the first player.

Similarly a mixed strategy \(\sigma_c^*\) of the column player is a best response to a row players’ strategy \(\sigma_r\) if and only if:

\[\sigma_c^*=\text{argmax}_{\sigma_c\in \mathcal{S}_2}\sigma_rB\sigma_c^T.\]

Question

For the Prisoners Dilemma:

What is the row player’s best response to either of the actions of the column player?

Answer

Recalling that \(A\) is given by:

\[\begin{split}A = \begin{pmatrix} 3 & 0\\ 5 & 1 \end{pmatrix}\end{split}\]

Against the first action of the column player the best response is to choose the second action which gives a utility of 5. This can be expressed as:

\[\text{argmax}_{i\in\mathcal{S}_1}A_{i1}=2\]

Against the second action of the column player the best response is to choose the second action which gives a utility of 1. This can be expressed as:

\[\text{argmax}_{i\in\mathcal{S}_1}A_{i2}=2\]

The row player’s best response to either of the actions of the column player is \(\sigma_r^*=(1,0)\). This can be expressed as:

\[\text{argmax}_{i\in\mathcal{S}_1}A_{ij}=2\text{ for all }j\in\mathcal{A}_2\]

Generic best responses in 2 by 2 games¶

In two player normal form games with \(|A_1|=|A_2|=2\): a 2 by 2 game, the utility of a row player playing \(\sigma_r=(x, 1 - x)\) against a strategy \(\sigma_c = (y, 1 - y)\) is linear in \(x\):

\[\begin{split}u_r(\sigma_r, \sigma_c) &= (x, 1 - x) A (y, 1 - y) ^T \\ &= A_{11}xy + A_{12}x(1-y) + A_{21}(1-x)y + A_{22}(1-x)(1-y) \\ &= a x + b\end{split}\]

where:

\[\begin{split}a &= A_{11}y + A_{12}(1 - y) - A_{21}y - A_{22}(1 - y)\\ b &= A_{21}y + A_{22}(1 - y)\end{split}\]

This observation allows us to obtain the best response \(\sigma_r^*\) against any \(\sigma_c = (y, 1 - y)\).

For example, consider Matching Pennies. Below is a plot of \(u_r(\sigma_r, \sigma_c)\) as a function of \(y\) for \(\sigma_r \in \{(1, 0), (0, 1)\}\).

(Source code, png, hires.png, pdf)

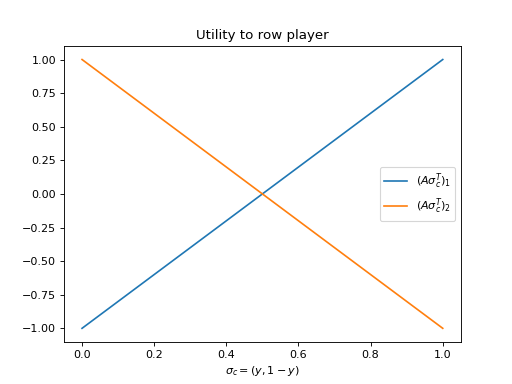
Given that the utilities in both cases are linear, the best response to any value of \(y \ne 1/2\) is either \((1, 0)\) or \((0, 1\). The best response \(\sigma_r^*\) is given by:

\[\begin{split}\sigma_r ^* = \begin{cases} (1, 0),& \text{ if } y > 1/2\\ (0, 1),& \text{ if } y < 1/2\\ \text{indifferent},& \text{ if } y=1/2 \end{cases}\end{split}\]

Question

For the Matching Pennies game:

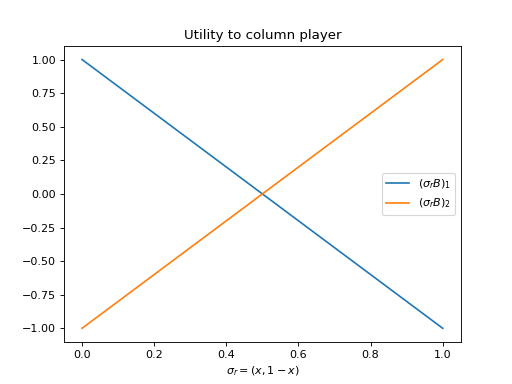
What is the column player’s best response as a function of \(x\) where \(\sigma_r=(x, 1 - x)\).

Answer

Recalling that \(B\) is given by:

\[\begin{split}B = \begin{pmatrix} -1 & 1\\ 1 & -1 \end{pmatrix}\end{split}\]

This gives:

\[\begin{split}u_c(\sigma_r, (1, 0)) =& -x + (1-x)= 1 - 2x\\ =& x - (1-x)= -1 + 2x\end{split}\]

Here is a plot of the utilities:

(Source code, png, hires.png, pdf)

General condition for a best response¶

In a two player game \((A,B)\in{\mathbb{R}^{m\times n}}^2\) a strategy \(\sigma_r^*\) of the row player is a best response to a column players’ strategy \(\sigma_c\) if and only if:

\[{\sigma_{r^*}}_i > 0 \Rightarrow (A\sigma_c^T)_i = \text{max}_{k \in \mathcal{A}_2}(A\sigma_c ^ T)_k \text{ for all }i \in \mathcal{A}_1\]

Proof¶

\((A\sigma_c^T)_i\) is the utility of the row player when they play their \(i^{\text{th}}\) action. Thus:

\[\sigma_rA\sigma_c^T=\sum_{i=1}^{m}{\sigma_r}_i(A\sigma_c^T)_i\]

Let \(u=\max_{k}(A\sigma_c^T)_k\) giving:

\[\begin{split}\sigma_rA\sigma_c^T&=\sum_{i=1}^{m}{\sigma_r}_i(u - u + (A\sigma_c^T)_i)\\ &=\sum_{i=1}^{m}{\sigma_r}_iu - \sum_{i=1}^{m}{\sigma_r}_i(u - (A\sigma_c^T)_i)\\ &=u - \sum_{i=1}^{m}{\sigma_r}_i(u - (A\sigma_c^T)_i)\end{split}\]

We know that \(u - (A\sigma_c^T)_i\geq 0\), thus the largest \(\sigma_rA\sigma_c^T\) can be is \(u\) which occurs if and only if \({\sigma_r}_i > 0 \Rightarrow (A\sigma_c^T)_i = u\) as required.

Question

For the Rock Paper Scissors game:

Which of the following pairs of strategies are best responses to each other:

\(\sigma_r=(0, 0, 1) \text{ and } \sigma_c=(0, 1/2, 1/2)\)
\(\sigma_r=(1/3, 1/3, 1/3) \text{ and } \sigma_c=(0, 1/2, 1/2)\)
\(\sigma_r=(1/3, 1/3, 1/3) \text{ and } \sigma_c=(1/3, 1/3, 1/3)\)

Answer

Recalling that \(A\) and \(B\) are given by:

\[\begin{split}A = \begin{pmatrix} 0 & -1 & 1 \\ 1 & 0 & -1\\ -1 & 1 & 0\\ \end{pmatrix}\end{split}\]

\[\begin{split}B = - A = \begin{pmatrix} 0 & 1 & -1 \\ -1 & 0 & 1\\ 1 & -1 & 0\\ \end{pmatrix}\end{split}\]

We can apply the best response condition to each pairs of strategies:

\(A\sigma_c^T = \begin{pmatrix}0\\ -1/2\\ 1/2\\\end{pmatrix}\). \(\text{max}(A\sigma_c^T)=1/2\). The only \(i\) for which \({\sigma_r}_i > 0\) is \(i=3\) and \((A\sigma_c^T)_3=\text{max}(A\sigma_c^T)\) thus \(\sigma_r\) is a best response to \(\sigma_c\). \(\sigma_rB = (1, -1, 0)\). \(\text{max}(\sigma_rB)=1\). The values of \(i\) for which \({\sigma_c}_i > 0\) are \(i=2\) and \(i=3\) but \((\sigma_r B)_2 \ne \text{max}(\sigma_r B)\) thus \(\sigma_c\) is not a best response to \(\sigma_r\).
\(A\sigma_c^T = \begin{pmatrix}0\\ -1/2\\ 1/2\\\end{pmatrix}\). \(\text{max}(A\sigma_c^T)=1/2\). The values of \(i\) for which \({\sigma_r}_i > 0\) are \(i=1\), \(i=2\) and \(i=3\) however, \((A\sigma_c^T)_2 \ne \text{max}(A\sigma_c^T)\) thus \(\sigma_r\) is not a best response to \(\sigma_c\). \(\sigma_rB = (0, 0, 0)\). \(\text{max}(\sigma_rB)=0\). The values of \(i\) for which \({\sigma_c}_i > 0\) are \(i=2\) and \(i=3\) and \((\sigma_r B)_2 = (\sigma_r B)_3= \text{max}(\sigma_r B)\) thus \(\sigma_c\) is a best response to \(\sigma_r\).
\(A\sigma_c^T = \begin{pmatrix}0\\ 0\\ 0\\\end{pmatrix}\). \(\text{max}(A\sigma_c^T)=0\). The values of \(i\) for which \({\sigma_r}_i > 0\) are \(i=1\), \(i=2\) and \(i=3\) and \((A\sigma_c^T)_1=(A\sigma_c^T)_2 = (A\sigma_c^T)_3 =\text{max}(A\sigma_c^T)\) thus \(\sigma_r\) is a best response to \(\sigma_c\). \(\sigma_rB = (0, 0, 0)\). \(\text{max}(\sigma_rB)=0\). The values of \(i\) for which \({\sigma_c}_i > 0\) are \(i=1\), \(i=2\) and \(i=3\) and \((\sigma_r B)_1 =(\sigma_r B)_2 = (\sigma_r B)_3= \text{max}(\sigma_r B)\) thus \(\sigma_c\) is a best response to \(\sigma_r\).

Definition of Nash equilibrium¶

In a two player game \((A, B)\in {\mathbb{R}^{m \times n}} ^ 2\), \((\sigma_r, \sigma_c)\) is a Nash equilibria if \(\sigma_r\) is a best response to \(\sigma_c\) and \(\sigma_c\) is a best response to \(\sigma_r\).

Using Nashpy¶

See Check if a strategy is a best response for guidance of how to use Nashpy to check if a strategy is a best response.